FUENTE IMAGEN: Termotips de Alexa

Una de sus aportaciones fue el teorema fundamental del álgebra, que dice:

«Todo polinomio de grado con coeficientes complejos tiene exactamente raíces complejas» (dicho de otra forma: todo polinomio de grado con coeficientes complejos tiene al menos una raíz compleja).

Destaco también en estadística, publicando Theoria combinationis observationum erroribus minimis obnoxiae, dedicada a la distribución normal (cuya representación gráfica de la función de densidad de dicha distribución se denomina campana de Gauss, pero de esto hablaremos en otro momento.

Centrémonos en el método de Gauss para triangular una matriz, que nos permite resolver sistemas de ecuaciones lineales con cualquier número de ecuaciones y de incógnitas.

Dado un sistema de tres ecuaciones con tres incógnitas x, y , z, a él están asociadas dos matrices:

A matriz de coeficientes y A* matriz ampliada (se le añade a la matriz de coeficientes la columna de términos independientes).

La idea utilizando el método de Gauss es tomar la matriz ampliada asociada al sistema y hacemos las trasformaciones de filas necesarias para hacer la matriz de coeficientes triangular (hacer ceros), a partir de ahí deducimos los valores de las variables.

Una vez obtenida la variable z en la tercera ecuación, llevar este valor de z a la segunda ecuación para obtener el valor de y, y así despejar la incógnita x en la primera ecuación, conocidos ya los valores de la z e y.

Estos sistemas se llaman escalonados o triangulares, y se resuelven de abajo a arriba.

FUENTE: sistema-de-ecuaciones-en-la-vida

Veamos un vídeotutorial, para entenderlo mejor, sacado del BLOG Yo soy tu profe

Para terminar mirar el siguiente documento con ejercicios resuelto y problemas donde hay que utilizar el método de Gauss EJERCICIOS RESUELTOS_Sistemas_gauss_2017

PARA SABER MAS: sistemas_ecuaciones_apuntes

Esta entrada participa en la Edición 7.7 del Carnaval de Matemáticas, que en esta ocasión organiza Los Matemáticos no son gente seria cuyo anfitrión es Juan Martínez-Tébar

La derivada es el ritmo de cambio de cualquier función en un determinado instante, pero también puede representar el ritmo o velocidad de cambio de cualquier cosa, la densidad o aumento de la población de delfines en relación con el aumento o disminución de la temperatura del agua, el ritmo de cambio de volumen de un globo respecto al área de su superficie o el ritmo de cambio del precio de una pizza con respecto a su tamaño.

La derivada dentro de la rama de la Física estudia las leyes del movimiento, lo que las ruedas son para un viaje, un medio sencillo pero muy eficaz.

Derivadas en la Vida cotidiana

DEFINICIÓN DE DERIVADA

VÍDEO Interpretación geométrica de la derivada

Si tenemos una función f(x), la derivada de la función en x=a, f ‘(a), es la pendiente de la recta tangente a f(x) en el punto de abscisa x=a.

De esta forma, si tenemos una función f(x), su función derivada f ‘(x) es la función que en cada punto toma el valor de la pendiente de la recta tangente a f(x) en ese punto.

Para entender el concepto de derivada necesitamos entender que es la tasa de variación y la tasa de variación media

1. Dada una función f(x), llamábamos tasa de variación al número que representa el aumento o disminución que experimenta la función al aumentar la variable independiente de un valor «a» a otro «b».
   La tasa de variación de f(x) entre a y b (siendo a<b) es igual a:       TV[a, b]= f(b)-f(a)

2. La tasa de variación media de una función f(x)entre a y b (siendo a<b), la definíamos como la variación media que se producía en el intervalo

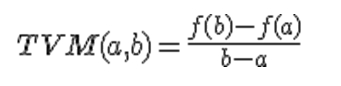
         La T.V.M. de una función en un intervalo [a,b] es igual a la pendiente de la recta secante a la gráfica de la función en puntos de abscisas a y b.

Ejemplo: https://www.youtube.com/watch?time_continue=1&v=Mk0Mr_ctdUA

RELACION TVM con la monotonía de una función

La tasa de variación media, TVM, de una función f(x) en un intervalo [a, b] es: TVM[a, b]

• Si f(x) es creciente en el intervalo (a, b), la tasa de variación media en [a, b] es positiva; es decir: f(x) creciente en (a, b) ……… TVM[a, b] > 0
• Si f(x) es decreciente en el intervalo (a, b), la tasa de variación media en [a, b] es negativa; es decir: f(x) decreciente en (a, b)………… TVM[a, b] < 0
•  Si f(x) es constante en el intervalo (a, b), la tasa de variación media en [a, b] es cero; es decir: f(x) constante en (a, b)…………… TVM[a, b] =0

COMO LLEGAMOS A LA DEFINICIÓN DE DERIVADA………………..

Partiendo de la TVM (a,b)

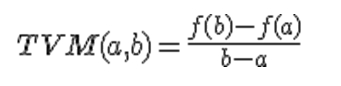
Si en lugar de «b», al segundo punto lo llamamos «a+h», la fórmula anterior quedaría así:

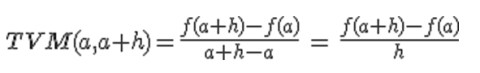
Fíjate que si manipulas los controles a y h de la derecha, puedes ver cómo cambia la TVM de esa función, pero en particular, es interesante que te fijes lo que ocurre si el intervalo donde hacemos la tasa de variación media es especialmente pequeño. Fíjate que nos reducimos prácticamente al punto a. Y mientras más pequeño, más nos reducimos

Si hacemos h muy muy muy pequeño, obtenemos una información precisa de lo que ocurre en el punto de abscisa a. Y hacer h muy pequeño, es hacerlo tender a cero. Pues bien cuando hacemos h tender a cero en la tasa de variación media, llegamos al concepto de tasa de variación instantánea. Es decir, la tasa de variación instantánea en un punto, es el límite cuando h tiende a cero de la tasa de variación media en el intervalo [a, a+h]

Y esto precisamente nos lleva al concepto de derivada en un punto; la variación instantánea en un punto. Así, la derivada de una función f(x) en el punto de abscisa x₀, se define como el límite:

Vídeo (calculo derivada de una función en un punto usando la definición de derivada)

Vídeo (cálculo derivada de una función usando la definición de derivada en un punto con un ejemplo de una función cuadrática)

Podemos sacar la ecuación de la recta tangente y normal o perpendicular a una curva en un punto, usando la ecuación punto-pendiente de la recta; la pendiente es f ‘(a) y el punto por el que pasa la recta (a, f(a)):

DEFINICIÓN MATEMÁTICA DE LA DERIVADA (con muchos deltas e incrementos, algo liosa para niveles bajos, pero muy muy interesante y bien explicado)

RESUMEN

1. DERIVADA DE LA FUNCIÓN EN UN PUNTO

La derivada de la función f en el punto x=a es el límite, si existe, que viene dado por:

Si el límite existe se dice que la función f es derivable en el punto x=a. La derivada de una función en un punto es un número real.

La derivada se puede representar mediante varias notaciones: f´(x), y´(x), D f(x)

En ciencias experimentales se suele emplear la expresión:

2. INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA

La pendiente de la tangente a una curva en un punto es igual a la derivada de la función en ese punto: m =  f´(a)

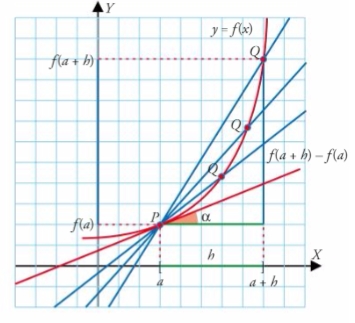
FUENTE IMAGEN: LIBRO Matemáticas Aplicadas Ciencias Sociales 1º Bachillerato. BRUÑO

La normal de una curva en un punto a es la perpendicular a la recta tangente en dicho punto.

3. REGLAS DE DERIVACIÓN

VIDEO EJERCICOS DERIVADAS BASICAS

LIBRO: Matemáticas Aplicadas a las Ciencias Sociales 1º Bachillerato. Editorial BRUÑO

TEMA9_DERIVADAS

SOLUCIONARIO_UD9_DERIVADAS

EJERCICIOS DERIVADAS_resueltos

EJERCICOS_VARIADOS_resueltos

Esta entrada participa en la edición 7.4 del Carnaval de Matemáticas, cuyo blog anfitrión es ::ZTFNews

FUENTES: http://www.ieszaframagon.com/matematicas/matematicas2/derivada/1_tasa_de_variacin_media_e_instantnea_definicin_de_derivada.html

http://www.infoymate.es/Bruno/

LIBRO: Matemáticas Aplicadas a las Ciencias Sociales 1º Bachillerato. Editorial BRUÑO